Question

An AC voltage of the form Δv = 95 sin 275t where Δv is in volts and t is in seconds, is applied to a series RLC circuit. If R = 38.0 Ω, C = 26.0 µF, and L = 0.240 H, find the following. (a) impedance of the circuit

1 Ω

(b) rms current in the circuit
2 A

(c) average power delivered to the circuit
3 W

Answer 1

(a) 83.06Ω

(b) 0.81A

(c) 25.0W

Step-by-step explanation:

Comparing Δv = 95 sin 275t with Δv = Vmaxsinωt

ω = 275

Inductive reactance Χ = ωL

= 275 × 0.240

= 66 Ω

Capacitive reactance Χ = 1/ωc

= 1/ (275 × 26 x 10^-6)

= 139.86Ω

Impedance Z =
`\sqrt{R^(2) + (wL - (1)/(wc) )^(2)`

=
`\sqrt{R^(2) + (X_(l) - X_(c) )^(2)`

=
`\sqrt{38^(2) + (66 - 139.86)^(2)`

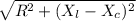
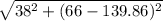
= 83.06Ω

(b)
`I_(rms) = (V_(rms))/(Z)`

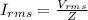
solving for
`V_(rms)`,

`V_(rms) = (V_(max))/(√(2))`

`V_(rms) = (95)/(√(2))`

`V_(rms) = 67.2V`

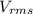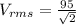
substituting the value of
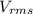`V_(rms)` and Z into
`I_(rms)` equation, we have;

`I_(rms) = (67.2)/(83.06)`

`I_(rms) = 0.81A`

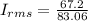
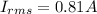
(c) Average power P =
`I_(rms)[\tex][tex]V_(rms)`cos∅

To get the average power, we first solve for ∅ since it was not given.

∅
`= tan^(-1)(X_(l) - X_(c))/(R)`

∅
`= tan^(-1)(66 - 139.86)/(38)`

∅
`= tan^(-1)(-73.86)/(38)`

∅
`= tan^(-1) -1.9437`

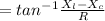
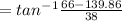
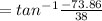
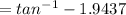
∅ = -62.77°

Average power P = 0.81 × 67.2 × cos-62.77

P = 0.81 × 67.2 × 0.46

P = 25.03872W

P = 25.0W