Question

A random sample of 1000 people was taken. Four hundred fifty of the people in the sample favored Candidate A. The 95% confidence interval for the true proportion of people who favor Candidate A is:_____

Answer 1

The 95% confidence interval would be given (0.419;0.481).

Explanation:

Data given and notation

n=1000 represent the random sample taken

X=450 represent the people in the sample favored Candidate A

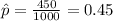`\hat p=(450)/(1000)=0.45` estimated proportion of people in the sample favored Candidate A

`\alpha=0.05` represent the significance level

Confidence =0.95 or 95%

p= population proportion of people in the sample favored Candidate A

Solution to the problem

The confidence interval would be given by this formula

`\hat p \pm z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

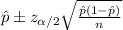
For the 95% confidence interval the value of
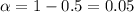`\alpha=1-0.5=0.05` and
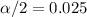`\alpha/2=0.025`, with that value we can find the quantile required for the interval in the normal standard distribution.

`z_(\alpha/2)=1.96`

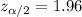
And replacing into the confidence interval formula we got:

`0.45 - 1.96 \sqrt{(0.45(1-0.45))/(1000)}=0.419`

`0.45 + 1.96 \sqrt{(0.45(1-0.45))/(1000)}=0.481`

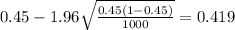
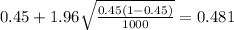
And the 95% confidence interval would be given (0.419;0.481).

We are confident (95%) that about 41.9% to 48.1% of the people are favored Candidate A.