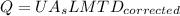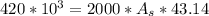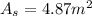Answer:
a)

b)
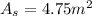
c)
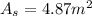
Step-by-step explanation:
Water in:
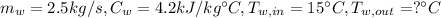
Process fluid in:
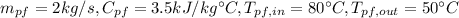
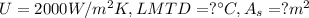
Step 1: Determine the rate of heat transfer in the heat exchanger
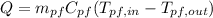
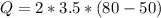
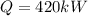
Step 2: Determine outlet temperature of water
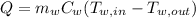
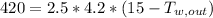
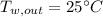
Part a) Parallel Flow
Step 3: Determine the Logarithmic Mean Temperature Difference (LMTD)
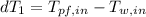
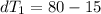
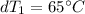
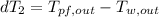
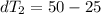
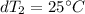
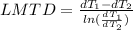
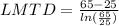
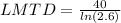
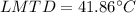
Step 4: Determine required surface area of heat exchanger

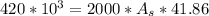

Part b) Counter Flow
Step 3: Determine the Logarithmic Mean Temperature Difference (LMTD)

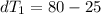
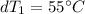
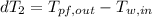
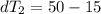

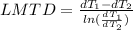
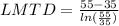
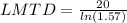

Step 4: Determine required surface area of heat exchanger

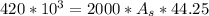
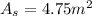
Part c) 1-2 shell and tube exchanger with the water on the shell side
Step 3: Determine the Logarithmic Mean Temperature Difference (LMTD) for counter flow

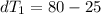
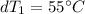
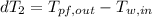
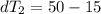

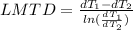
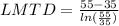
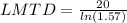

Step 4: Determine LMTD Correction Factor and Corrected LMTD

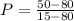
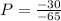
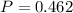
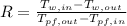
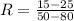


Correction factor F can be determined from attached graph using P and F values calculated above
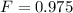
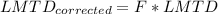
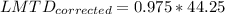
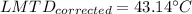
Step 5: Determine required surface area of heat exchanger