Question

A sample of an unknown gas takes 371 s to diffuse through a porous plug at a given temperature.

At the same temperature, N2(g) takes 175 s to diffuse through the same plug.

What is the molar mass of the unknown gas?

Answer 1

125.84 g/mol is the molar mass of the unknown gas.

Step-by-step explanation:

Let the volume of the gases effusing out be V.

Effusion rate of the unknown gas =
`R=(V)/(371 s)`

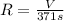
Effusion rate of the nitrogen gas =
`r=(V)/(175 s)`

Molar mass of unknown gas = m

Mass of nitrogen gas = 28 g/mol

Graham's law states that the rate of effusion or diffusion of gas is inversely proportional to the square root of the molar mass of the gas. The equation given by this law follows the equation:

`\text{Rate of diffusion}\propto \frac{1}{\sqrt{\text{Molar mass of the gas}}}`

`(R)/(r)=\sqrt{(28 g/mol)/(M)}`

`((V)/(371 s))/((V)/(175s))=\sqrt{(28 g/mol)/(M)}`

`(175 s)/(371 s)=\sqrt{(28 g/mol)/(M)}`

`M=(28 g/mol* 371* 371)/(175* 175)=125.84 g/mol`

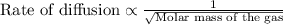
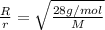
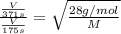
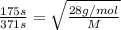
125.84 g/mol is the molar mass of the unknown gas.