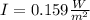A portable audio speaker has a power output of 8.00 W. If the speaker emits sound equally in all directions, what is the sound intensity at a distance of 2.00 m from the speaker…

Question

asked Apr 20, 2020 232k views

1 Answer

Daria Pydorenko · Answer 1 · 2020-04-27T07:21:33+0000

Answer:

I=0.159(W)/(m^2)

Step-by-step explanation:

the formula to calculate the intensity, given the power:

I=(P)/(A)

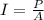
Where
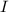is intensity, and
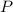is the power that the wave carries in a given area
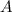. In this case:

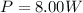P=8.00W , and the area since the speaker emits the sound equally in all directions is the area of a surface of a sphere with a radius of
2.00m :

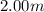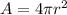
$A=4\pi r^2$

replacing the radius value:

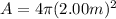
$A=4\pi (2.00m)^2$

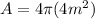
$A=4\pi (4m^2)$

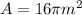
$A=16\pi m^2$

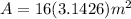
A=16(3.1426)m^2

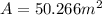
A=50.266m^2

So, now that we know the area we can calculate the intensity:

I=(P)/(A)

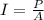
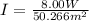
I=(8.00W)/(50.266m^2)

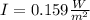
I=0.159(W)/(m^2)

the sound intensity at the distance of 2.00m from the speaker is
I=0.159(W)/(m^2)