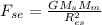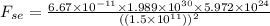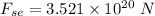Answer:
(a)
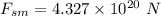
(b)
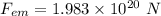
(c)
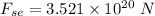
Solution:
As per the question:
Mass of Earth,
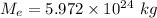
Mass of Moon,
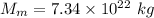
Mass of Sun,
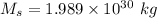
Distance between the earth and the moon,
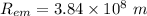
Distance between the earth and the sun,
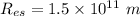
Distance between the sun and the moon,
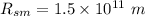
Now,
We know that the gravitational force between two bodies of mass m and m' separated by a distance 'r' is given y:
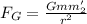 (1)
(1)
Now,
(a) The force exerted by the Sun on the Moon is given by eqn (1):
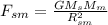
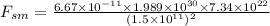
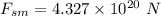
(b) The force exerted by the Earth on the Moon is given by eqn (1):
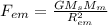

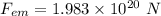
(c) The force exerted by the Sun on the Earth is given by eqn (1):