Answer:
The value of car after n years at the depreciation rate is $ 50,000
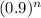 .
.
Explanation:
Given as :
The cost of the car that Jill bought = $ 50,000
The depreciation rate of car value = r = 10 % a years
Let The car after n years of depreciation = $ A
Now, According to question
The cost of car after n years of depreciation = initial cost of car ×
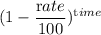
Or, $ A = $50,000 ×
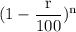
Or, $ A = $50,000 ×
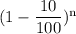
Or, $ A = $50,000 ×
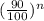
I.e $ A = $50,000 ×
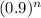
So, value of car after n years = $ 50,000
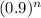
Hence The value of car after n years at the depreciation rate is $ 50,000
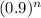 . Answer
. Answer