Question

A solenoid of length 0.700m having a circular cross-section of radius 5.00cm stores 6.00 μJ of energy when a 0.400-A current runs through it.

What is the winding density of the solenoid? (μ0 = 4π*10-7 T*m/A)

A) 865 turns/m

B) 327 turns/m

C) 1080 turns/m

D) 104 turns/m

E) 472 turns/m

Answer 1

The winding density of the solenoid is 104 turns/m.

(D) is correct option.

Step-by-step explanation:

Given that,

Length = 0.700 m

Radius = 5.00 cm

Energy = 6.00 μJ

Current = 0.400 A

We need to calculate the density of the solenoid

Using formula of the energy store

`E=(B^2)/(2\mu_(0))Al`

Put the value of magnetic field

`E=((\mu_(0)ni)^2)/(2\mu_(0))Al`

`n=\sqrt((2E)/(\mu_(0)i^2Al))`

Put the value into the formula

`n=\sqrt{(2*6.00*10^(-6))/(4\pi*10^(-7)*(0.4)^2*\pi*(5.00*10^(-2))^2*0.700)}`

`n=104\ turns/m`

Hence, The winding density of the solenoid is 104 turns/m.

Answer 2

The winding density of the solenoid, n = 104 turns/m

Step-by-step explanation:

Given that,

Length of the solenoid, l = 0.7 m

Radius of the circular cross section, r = 5 cm = 0.05 m

Energy stored in the solenoid,
`E=6\ \mu J=6* 10^(-6)\ J`

Current, I = 0.4 A

To find,

The winding density of the solenoid.

Solution,

The expression for the energy stored in the solenoid is given by :

`U=(1)/(2)LI^2`

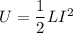
Where

L is the self inductance of the solenoid

`L=\mu_on^2lA`

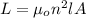
n is the winding density of the solenoid

`n=\sqrt{(2U)/(\mu_oI^2l\pi r^2)}`

`n=\sqrt{(2* 6* 10^(-6))/(4\pi * 10^(-7)* 0.7* (0.4)^2\pi (0.05)^2)}`

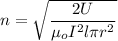
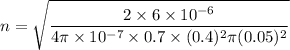
n = 104 turns/m

So, the winding density of the solenoid is 104 turns/m