Question

The value of Eºcell for the reaction Zn(s) + Cu2+(aq) <=> Zn2+(aq) + Cu(s) is 1.10 V. What is the value of E for a cell in which [Zn2+] = 1.0 x 10-3 M and [Cu2+] = 1.0 M?

Answer 1

Answer: The cell potential of the above reaction is 1.2 V

Step-by-step explanation:

The given chemical reaction follows:

`Zn(s)+Cu^(2+)(aq.)\rightarrow Zn^(2+)(aq.)+Cu(s)`

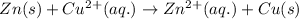
Oxidation half reaction:
`Zn(s)\rightarrow Zn^(2+)+2e^-`

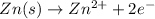
Reduction half reaction:
`Cu^(2+)+2e^-\rightarrow Cu(s)`

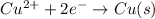
To calculate the EMF of the cell, we use the Nernst equation, which is:

`E_(cell)=E^o_(cell)-(0.059)/(n)\log ([Zn^(2+)])/([Cu^(2+)])`

where,

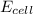`E_(cell)` = electrode potential of the cell = ? V

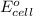`E^o_(cell)` = standard electrode potential of the cell = 1.1 V

n = number of electrons exchanged = 2

`[Cu^(2+)]=1.0M`

`[Zn^(2+)]=1.0* 10^(-3)M`

Putting values in above equation, we get:

`E_(cell)=1.1-(0.059)/(2)* \log((1.0* 10^(-3))/(1.0))\\\\E_(cell)=1.2V`

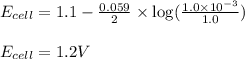
Hence, the cell potential of the above reaction is 1.2 V