Question

Find the angle of elevation of the sun from the ground when a tree that is 10 yards tall cast a shadow 14 yards long. Round to the nearest degree

Answer 1

The angle of elevation of the sun from the ground to the top of a tree is 36 degrees

Solution:

Given that a tree that is 10 yards tall cast a shadow 14 yards long

To find: angle of elevation of sun

The figure is attached below

In the figure, AB represents the height of tree

BC represents the length of shadow cast by tree

We have to find angle of elevation θ

Now by using trignometric identity,

`tan\theta =(Perpendicular)/(Base)`

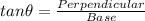
From the figure,

AB = Perpendicular = 10 yards

BC = Base = 14 yards

`tan\theta =(AB)/(BC)`

`tan \theta = (10)/(14)`

`\theta =tan^(-1)((10)/(14))\\\\\theta =36^(\circ)`

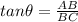
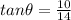
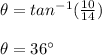
Thus the angle of elevation of sun from ground to top of tree is 36 degrees