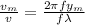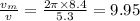Question

A sinusoidal transverse wave of amplitude ym = 8.4 cm and wavelength = 5.3 cm travels on a stretched cord. Find the ratio of the maximum particle speed (the speed with which a single particle in the cord moves transverse to the wave) to the wave speed.

Answer 1

The ratio is 9.95

Solution:

As per the question:

Amplitude,
`y_(m) = 8.4\ cm`

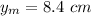
Wavelength,
`\lambda = 5.3\ cm`

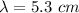
Now,

To calculate the ratio of the maximum particle speed to the speed of the wave:

For the maximum speed of the particle:

`v_(m) = y_(m)* \omega`

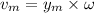
where

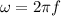`\omega = 2\pi f` = angular speed of the particle

Thus

`v_(m) = 2\pi fy_(m)`

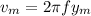
Now,

The wave speed is given by:

`v = f\lambda`

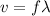
Now,

The ratio is given by:

`(v_(m))/(v) = (2\pi fy_(m))/(f\lambda)`

`(v_(m))/(v) = (2\pi * 8.4)/(5.3) = 9.95`