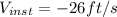Question

If a ball is thrown into the air with a velocity of 38 ft/s, its height in feet t seconds later is given by y = 38t − 16t2. (a) Find the average velocity for the time period beginning when t = 2 and lasting for each of the following.

(i) 0.5 seconds ft/s

(ii) 0.1 seconds ft/s

(iii) 0.05 seconds ft/s

(iv) 0.01 seconds ft/s

(b) Estimate the instantaneous velocity when t = 2. ft/s

Answer 1

i.-34ft/s

ii.-27.6ft/s

iii.-26.8ft/s

iv-26.7ft/s

B.-26ft/s

Explanation:

`average velocity = (y_(2)-y_(1))/(t_(2)-t_(1))\\`

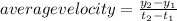
For all cases the value of the initial time
`t_(1) =2 seconds \\`

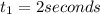
now we also use this time ti determine the value of the initial height in all cases

`y_(1)=38(2)-16(2)^(2) \\y_(1)= 12ft\\`

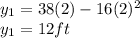
now when the time is increase by 0.5 seconds the new height becomes

`y_(2)=38(2.5)-16(2.5)^(2) \\y_(2)=-5fts\\`

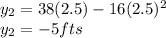
the velocity becomes

`[tex]Average velocity = (-5-12)/(2.5-2)\\Average velocity = -34ft/s\\`

ii. when the time is increase by 0.1 seconds

the new height becomes

`y_(2)=38(2.1)-16(2.1)^(2) \\y_(2)= 10.66ft\\`

`Average velocity = (10.66-12)/(2.05-2)\\Average velocity = -27.6ft/s\\`

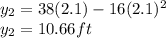
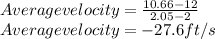
iii. when the time is increase by 0.05 seconds

the new height becomes

`y_(2)=38(2.05)-16(2.05)^(2) \\y_(2)= 9.24ft\\`

`Average velocity = (9.24-12)/(2.05-2)\\Average velocity = -26.8ft/s\\`

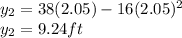
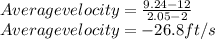
iv. when the time is increase by 0.1 seconds

the new height becomes

`y_(2)=38(2.01)-16(2.01)^(2) \\y_(2)= 11.73ft\\`

`Average velocity = (11.73-12)/(2.01-2)\\Average velocity = -26.7ft/s\\`.

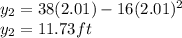
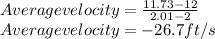B. For us to determine the instantaneous velocity expression, we differentiate the expressing for the height

`V_(inst)=38-32t\\`

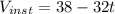
we now substitute t=2, we arrive at

`V_(inst)=-26ft/s\\`