Question

A uniform ladder of length l rests against a smooth, vertical wall. If the coefficient of static friction is 0.50, and the ladder makes a 53⁰ angle with respect to the horizontal, how far along the length of the ladder can a 56.0-kg person climb before the ladder begins to slip? The ladder is 7.5 m in length and has a mass of 21 kg.

Answer 1

X = 5.44 m

Step-by-step explanation:

First we can calculate the normal force acting from the floor to the ladder.

W₁+W₂ = N

W1 is the weigh of the ladder

W2 is the weigh of the person

So we have:

`m1g+m2g=N`

`N=755.37 N`

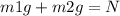
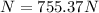
The friction force is:

`F_(force)=\mu N=0.5\cdot 755.37=377.68 N`

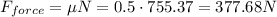
Now let's define the conservation of torque about the foot of the ladder:

`\tau_(ledder)+\tau_{person=\tau_(reaction)}`

`m_(1)\cdot g\cdot X \cdot cos(53)+m_(2)\cdot g\cdot 3.75 \cdot cos(53)=F_(force)7.5sin(53)`

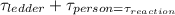
Solving this equation for X, we have:

`X = (377.68\cdot 7.5\cdot sin(53)-21\cdot 9.81\cdot 3.75 \cdot cos(53))/(56\cdot 9.81\cdot cos(53))`

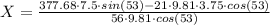
Finally, X = 5.44 m

Hope it helps!