Answer:
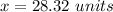
Explanation:
Given:
Expression for Pythagorean theorem:
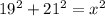
By Pythagorean theorem (applied to right triangles only):

where
 represents hypotenuse or the longest side of triangle, while
represents hypotenuse or the longest side of triangle, while
 and
and
 represents the other two sides of the triangle.
represents the other two sides of the triangle.
Solving for hypotenuse i.e.
 in the given expression
in the given expression
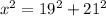
⇒
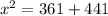
⇒
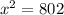
Taking square root both sides:
⇒
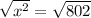
∴
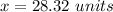 (Answer)
(Answer)