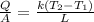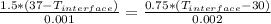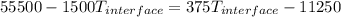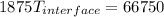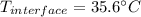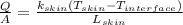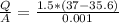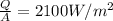Answer:
a) Thermal conductivity of skin:

b) Temperature of interface:
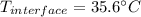
Heat flux through skin:
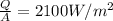
Step-by-step explanation:
a)
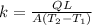
Where:
 is thermal conductivity of a material,
is thermal conductivity of a material,
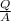 is heat flux through a material,
is heat flux through a material,
 is the thickness of the material,
is the thickness of the material,
 is the temperature on the first side and
is the temperature on the first side and
 is the temperature on the second side
is the temperature on the second side
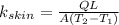
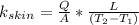
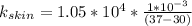

b)
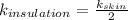
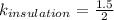
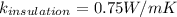
The heat flux between both surfaces is constant, assuming the temperature is maintained at each surface.