Question

A wooden boat discovered just south of the Great Pyramid in Egypt has a carbon-14/carbon-12 ratio that is 71.5% of that found in living organisms

Answer 1

2772.5 years

Step-by-step explanation:

Using the equation for radioactive decay of material:

`ln (N)/(N_(o) ) = -k*t`

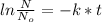
Where:

N is the amount of the material at time t,
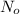`N_(o)` is the original amount of the material, and k is the rate constant.

The value if the rate constant (k) = 0.693/
`t_(1/2)`

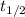
Where:

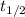`t_(1/2)` is the half life = 5730 years.

Then k = 0.693/5730 = 0.000121 (1/year)

Then solving for 't', we have:

`ln(71.5)/(100) = -0.000121*t`

t = -0.3355/-0.000121 = 2772.5 years

Therefore, the wooden boat is 2772.5 years old.