Question

The graph of y > 1 2 x - 2 is shown. Which set contains only points that satisfy the inequality? A) {(6, 1), (-1, -3), (4, 4)} B) {(1, -1), (-3, -3), (2, 4)} C) {(1, -1), (-3, -3), (4, -2)} D) {(-1, -3), (-3, -3), (2, 4)}

Answer 1

Option B) {(1, -1), (-3, -3), (2, 4)}

Explanation:

The correct inequality is

`y>(1)/(2)x-2`

The solution of the inequality is the shaded area above the dashed line
`y=(1)/(2)x-2`

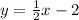
see the attached figure to better understand the problem

we know that

If a ordered pair satisfy the inequality, then the ordered pair must lie in the shaded area of the solution

Verify each case

case A) {(6, 1), (-1, -3), (4, 4)}

ordered pair (6,1)

For x=6, y=1

substitute in the inequality

`1>(1)/(2)(6)-2`

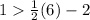
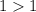`1>1` ---> is not true

therefore

The point not satisfy the inequality

case B) {(1, -1), (-3, -3), (2, 4)}

ordered pair (1,-1)

For x=1, y=-1

substitute in the inequality

`-1>(1)/(2)(1)-2`

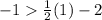
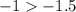`-1>-1.5` ---> is true

so

The point satisfy the inequality

ordered pair (-3,3)

For x=-3, y=3

substitute in the inequality

`3>(1)/(2)(-3)-2`

`3>-3.5` ---> is true

so

The point satisfy the inequality

ordered pair (2,4)

For x=2, y=4

substitute in the inequality

`4>(1)/(2)(2)-2`

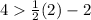
`4>-1` ---> is true

so

The point satisfy the inequality

therefore

The set contains only points that satisfy the inequality

case C) {(1, -1), (-3, -3), (4, -2)}

ordered pair (4,-2)

For x=4, y=-2

substitute in the inequality

`-2>(1)/(2)(4)-2`

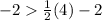
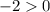`-2>0` ---> is not true

therefore

The point not satisfy the inequality

case D) {(-1, -3), (-3, -3), (2, 4)}

ordered pair (-1,-3)

For x=-1, y=-3

substitute in the inequality

`-3>(1)/(2)(-1)-2`

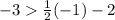
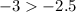`-3>-2.5` ---> is not true

therefore

The point not satisfy the inequality