Question

Approximate the area under the curve over the specified interval by using the indicated number of subintervals (or rectangles) and evaluating the function at the right-hand endpoints of the subintervals. (See Example 1.)f(x) = 9 − x2 from x = 1 to x = 3; 4 subintervals

Answer 1

The area under the function
`\int\limits^3_1 {9-x^2} \, dx \approx 7.25.`.

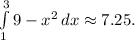Explanation:

We want to find the Riemann Sum for
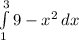`\int\limits^3_1 {9-x^2} \, dx` with 4 sub-intervals, using right endpoints.

A Riemann Sum is a method for approximating the total area underneath a curve on a graph, otherwise known as an integral.

The Right Riemann Sum is given by:

`\int_(a)^(b)f(x)dx\approx\Delta{x}\left(f(x_1)+f(x_2)+f(x_3)+...+f(x_(n-1))+f(x_(n))\right)`

where
`\Delta{x}=(b-a)/(n)`

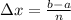
From the information given we know that a = 1, b = 3, n = 4.

Therefore,
`\Delta{x}=(3-1)/(4)=(1)/(2)`

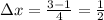
We need to divide the interval [1, 3] into 4 sub-intervals of length
`\Delta{x}=(1)/(2)`:

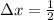`\left[1, (3)/(2)\right], \left[(3)/(2), 2\right], \left[2, (5)/(2)\right], \left[(5)/(2), 3\right]`

Now, we just evaluate the function at the right endpoints:

`f\left(x_(1)\right)=f\left((3)/(2)\right)=(27)/(4)=6.75`

`f\left(x_(2)\right)=f\left(2\right)=5=5`

`f\left(x_(3)\right)=f\left((5)/(2)\right)=(11)/(4)=2.75`

`f\left(x_(4)\right)=f(b)=f\left(3\right)=0=0`

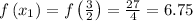
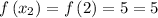
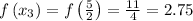
Next, we use the Right Riemann Sum formula

`\int\limits^3_1 {9-x^2} \, dx \approx (1)/(2)(6.75+5+2.75+0)=7.25`