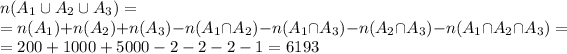Answer:
a. 4600
b. 6200
c. 6193
Explanation:
Let
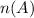 the number of elements in A.
the number of elements in A.
Remember, the number of elements in
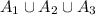 satisfies
satisfies
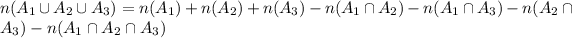
Then,
a) If
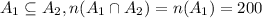 , and if
, and if
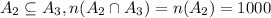
Since
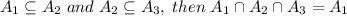
So
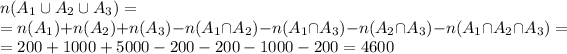
b) Since the sets are pairwise disjoint
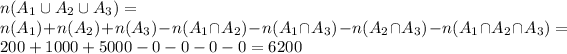
c) Since there are two elements in common to each pair of sets and one element in all three sets, then