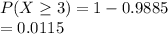Answer:
0.5987,0.3151,0.9885,0.0115
Explanation:
Given that a manufacturing company regularly conducts quality control checks at specified periods on the products it manufactures. Historically, the failure rate for LED light bulbs that the company manufactures is 5%
Let X be the no of defectives in the sample of 10
X is binomial since each bulb is independent of the other and there are only two outcomes
P(X=x) =
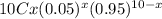
Using the above we calculate
a) P(X=0) =
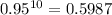
b) P(X=1)
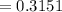
c)
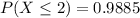
d)