Question

A solution of sodium chloride in water has a vapor pressure of 17.5 torr at 25°C. What is the mole fraction of NaCl solute particles in this solution? What would be the vapor pressure of this solution at 45°C? The vapor pressure of pure water is 23.8 torr at 25°C and 71.9 torr at 45°C and assume sodium chloride exists as Na⁺ and Cl⁻ ions in solution.

Answer 1

Step-by-step explanation:

Since, NaCl exists as
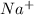`Na^(+)` and
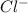`Cl^(-)` in solution. Therefore, Van't Hoff factor (i) will be equal to 2.

Now, we assume that there are "n" moles of NaCl in the given solution. And, we assume that there is 1 kg of solvent (water).

So,
`(\Delta P)/(P) = i * \frac{\text{no. of moles of NaCl}}{\text{Mass of water in kg}}`

`(23.8 torr - 17.5 torr)/(23.8 torr) = 2 * (n)/(1)`

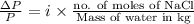
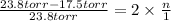
0.264 =
`2 * (n)/(1)`

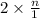
n = 0.132

Also, moles of water will be calculated as follows.

Moles of water =
`(1000)/(18)`

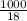
= 55.56 mol

Hence, mole fraction of NaCl is calculated as follows.

Mole fraction =
`(0.132)/(55.56 + 0.132)`

=
`2.37 * 10^(-3)`

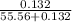
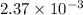
Hence, mole fraction of NaCl will be
`2.37 * 10^(-3)`.

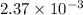At
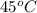`45^(o)C`, the vapor pressure will be calculated as follows.

`(71.9 - p)/(71.9) = 2 * \frac{n}{\text{mass of water in kg}}`

`(71.9 - p)/(71.9) = 2 * (0.132)/(1)`

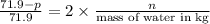
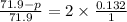
71.9 - p = 18.98

p = 52.92 torr

Therefore, vapor pressure of the given solution is 52.92 torr.