Question

A solid box made from a material whose density is rhoS floats with two thirds of its volume submerged in a liquid whose density is rhoL. How do the two densities compare?

Answer 1

`(\rho_S)/(\rho_L) = (2)/(3)`

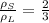
Step-by-step explanation:

density of the solid box material =
`\rho_s`

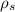
density of the liquid material =
`\rho_L`

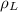
Given that

solid box floats with two thirds of its volume submerged in a liquid

let V be the volume of the box

then,

`V\rho_sg= (2V)/(3)\rho_L g`

⇒
`(\rho_S)/(\rho_L) = (2)/(3)`

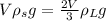
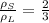
so, the ratio of densities of solid and and the liquid is 2/3