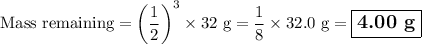Answer:
Step-by-step explanation:
The half-life of chromium-51 (28 da) is the time it takes for half of it to decay.
After one half-life, half of the original amount will remain.
After a second half-life, half of that amount will remain, and so on.
We can construct a table as follows:

We see that, after 84 da (three half-lives), ⅛ of the original mass remains.