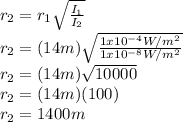Question

At a distance of 14.0 m from a point source, the intensity level is measured to be 80 dB. At what distance from the source will the intensity level be 40 dB

Answer 1

1400m

Step-by-step explanation:

For spherical waves we can use the following relationship between distance and intensity:

`(I_(1))/(I_(2))=(r_(2)^2)/(r_(1)^2)`

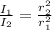
Where
`I_(1)` and
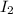`I_(2)` are the first and second intensity, in
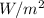`W/m^2`. And
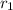`r_(1)` is the first distance:
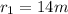`r_(1)=14m` , and
`r_(2)` the distace we want to find.

Clearing the previous equation or
`r_(2)`

`r_(2)^2=(I_(1)r_(1)^2)/(I_(2)) \\r_(2)=\sqrt{(I_(1)r_(1)^2)/(I_(2))} \\r_(2)=r_(1)\sqrt{(I_(1))/(I_(2))}`.

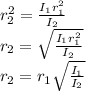This is what we will be using to find the answer, but fist we must convert the quantities 80dB and 40dB to
`W/m^2`

We will call the quantities in dB
`\beta_(1)` and
`\beta _(2)`:

`\beta_(1)=80dB`

`\beta_(2)=40dB`

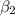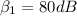
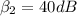
We will use the following to find the corresponding intensities
`I_(1)` and
`I_(2)`:

`\beta_(1)=10log(I_(1))/(I_(o))`

`\beta_(2)=10log(I_(2))/(I_(o))`

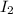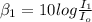
for both of these:
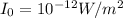`I_(0)=10^(-12)W/m^2`, and it is the minimum intensity that a human being perceives.

Thus, for
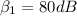`\beta_(1)=80dB` we have:

`80dB=10log(I_(1))/(I_(o))`

`8dB=log(I_(1))/(I_(o))`

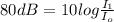
And to eliminate the logarithm, we use its inverse operation, exponentiation.

`10^8=10^{log(I_(1))/(I_(0)) }`

`10^8=(I_(1))/(I_(0))`

`I_(0)(10^8)=I_(1)`

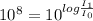
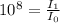
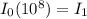
replacing
`I_(0)=10^(-12)W/m^2`:

`10^(-12)W/m^2(10^8)=I_(1)`

`1x10^(-4)W/m^2=I_(1)`

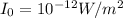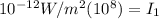
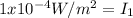
and similarly for
`I_(2)`

`40dB=10log(I_(2))/(I_(o))`

`4dB=log(I_(2))/(I_(o))`

`10^4=10^{log(I_(2))/(I_(0)) }`

`10^4=(I_(2))/(I_(0))`

`I_(0)(10^4)=I_(2)`

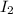
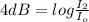
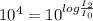
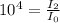
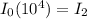
replacing
`I_(0)=10^(-12)W/m^2`:

`10^(-12)W/m^2(10^4)=I_(2)`

`1x10^(-8)W/m^2=I_(2)`

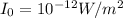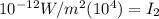
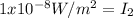
Now we substitute in the equation we had found for
`r_(2)`

`r_(2)=r_(1)\sqrt{(I_(1))/(I_(2))}\\r_(2)=(14m)\sqrt{(1x10^(-4)W/m^2)/(1x10^(-8)W/m^2)}\\r_(2)=(14m)√(10000)\\ r_(2)=(14m)(100)\\r_(2)=1400m`

Answer 2

`d_2=19.8m`

Step-by-step explanation:

The problem can be solved easily, because the relationship between intensities
`I_1` and
`I_2` at distances
`d_1` and
`d_2` respectively can be written as:

`(I_2)/(I_1) =(d_1^2)/(d_2^2)`

Where:

`I_1=Intensity\hspace{3}1\\I_2=Intensity\hspace{3}2\\d_1=Distance\hspace{3}1\\d_2=Distance\hspace{3}2`

In this case:

`I_1=80dB\\I_2=40dB\\d_1=14m\\d_2=?`

Solving for
`d_2`

`d_2=\sqrt{(d_1^2 *I_1)/(I_2) } =\sqrt{(14^2*80)/(40) } =√(392) =19.79898987m\approx19.8m`