Answer:
The intercept of the given points is -
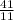
Explanation:
Given points as :
(
 ,
,
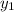 ) = (
) = (
 , - 7 )
, - 7 )
(
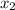 ,
,
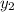 ) = ( - 4 , 5 )
) = ( - 4 , 5 )
Now, slope of line using given points can be written as :
Slope = m =

or. m =
/(2)]() }[/tex]
}[/tex]
or, m =
/(2)]() }[/tex]
}[/tex]
or, m =
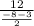
Or, m =
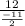
∴ m =

So, The slope of the line using points = m =

now, equation of line in slope intercept form can be written as
y -
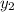 = m × ( x -
= m × ( x -
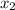 )
)
or, y - 5 =
 × ( x - ( - 4 ) )
× ( x - ( - 4 ) )
or, y - 5 =
 × ( x + 4 )
× ( x + 4 )
Or, 11 × ( y - 5 ) = - 24 × ( x + 4 )
Or, 11 y - 55 = - 24 x - 96
Or, 11 y = - 24 x - 96 + 55
Or, 11 y = - 24 x - 41
∴ y =
 x -
x -
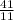
Now, comparing with slope intercept equation
I.e y = m x + c , where c is the intercept
So, The intercept of points is -
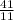
Hence The intercept of the given points is -
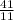 Answer
Answer