Question

A tennis player keeps track of the number of successful first serves he makes. During the first 8 service points of a game, only 2 of his first serves are playable, so his first serve percentage is 25%. How many more consecutive successful first serves must he have to raise his first serve percentage to 60%?

Answer 1

He needs 7 more consecutive successful first serves to raise his first serve percentage to 60%.

Explanation:

After n consecutive serves, his total number of serves is going to be n+8, since he has already served 8 times. In the best case, his number of successful first serves is n+2.

His percentage of succesful first serves is the division of the number of succesful first serves divided by the total number of serves. So

`P = (n+2)/(n+8)`

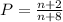
We want
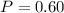`P = 0.60`. So

`0.6 = (n+2)/(n+8)`

`n+2 = 0.6*(n+8)`

`n + 2 = 0.6n + 4.8`

`n - 0.6n = 4.8 - 2`

`0.4n = 2.8`

`n = (2.8)/(0.4)`

`n = 7`

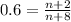
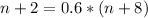
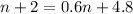
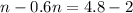
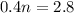
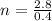
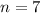
He needs 7 more consecutive successful first serves to raise his first serve percentage to 60%.