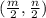Answer:
DE = m unit , Slope DE = 0 , Mid point of DE =
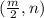
EF = n unit , Slope EF = Undefined , Mid point of EF =
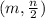
DF = √(m²+n²) unit , Slope DF = -n / m, Mid point of DF =
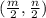
Explanation:
Given:
point D( x₁ , y₁) ≡ ( 0 ,n)
point E( x₂ , y₂) ≡ (m , n)
point F( x₃ , y₃) ≡ ( m ,0)
To Find:
DE = ? , Slope DE = ? , Mid point of DE = ?
EF = ? , Slope EF = ? , Mid point of EF = ?
DF = ? , Slope DF = ? , Mid point of DF = ?
Solution:
We will use Distance Formula,Slope Formula, and Section Formula.
Distance Formula:
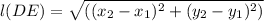
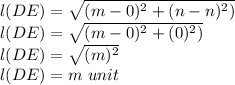
Similarly,
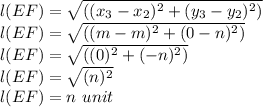
Similarly,
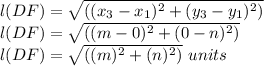
Slope Formula:
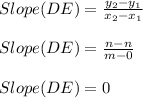
Similarly,
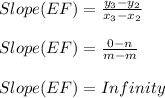
Similarly,
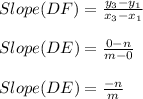
Section Formula:
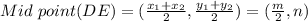
Similarly,
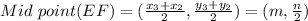
Similarly,
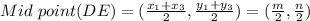
DE = m unit , Slope DE = 0 , Mid point of DE =
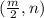
EF = n unit , Slope EF = Undefined , Mid point of EF =
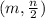
DF = √(m²+n²) unit , Slope DF = -n / m, Mid point of DF =