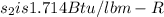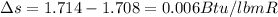Answer:
A)
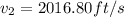
B)
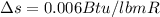
Step-by-step explanation:
Given data:
P-1 = 100 lbf/in^2
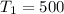 degree f
degree f
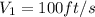
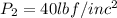
effeciency = 80%
from steady flow enerfy equation
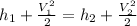
where h1 and h2 are inlet and exit enthalpy
for P1 = 100 lbf/in^2 and T1 = 500 degree F
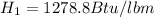
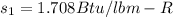
for P1 = 40 lbf/in^2
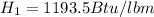
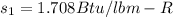
exit enthalapy h_2
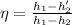
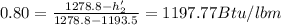
from above equation
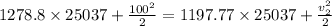 [1 Btu/lbm = 25037 ft^2/s^2]
[1 Btu/lbm = 25037 ft^2/s^2]
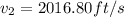
b) amount of entropy
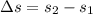
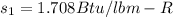
at
![h_2 = 1197.77 Btu/lbm [\tex] and [tex]P_2 = 40 lbf/in^2](https://img.qammunity.org/2020/formulas/engineering/college/bs4w5k4xik5mkvclhf834c6hsjcfjwy7ad.png)