Question

A statistics professor plans classes so carefully that the lengths of her classes are uniformly distributed between 45.0 and 55.0 minutes. Find the probability that a given class period runs between 50.25 and 50.5 minutes.

Answer 1

Answer: 0.025

Explanation:

The probability density function for a random variable that is uniformly distributed on interval [a,b] is given by :-

`f(x)=(1)/(b-a)`

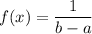
Given : A statistics professor plans classes so carefully that the lengths of her classes are uniformly distributed between 45.0 and 55.0 minutes.

Let x be the random variable that denotes the lengths of her classes.

Then, the probability density function =
`f(x)=(1)/(55-45)=(1)/(10)`

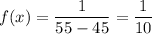
Now, the probability that a given class period runs between 50.25 and 50.5 minutes will be :-

`P(50.25<x<50.5)=\int^(50.5)_(50.25)\ f(x)\ dx\\\\=\int^(50.5)_(50.25)\ (1)/(10)\ dx\\\\= (1)/(10)[x]^(50.5)_(50.25)\\\\=(1)/(10)[50.5-50.25]\\\\=(1)/(10)[0.25]=0.025`

Hence, the required probability =0.025