Answer:
Sam invested $1200 at 8% and $600 at 6%
Explanation:
A linear system with two equations can be modeled from the information given. Let 'x' be the amount invested at 8% and 'y' the amount invested at 6%
The sum of both amounts invested at an 8% rate and 6% rate equals 1800
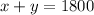
The yearly income on the 8% investment was $24 more than twice the income from the 6%
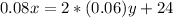
Solving the linear system:
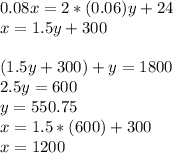
Sam invested $1200 at 8% and $600 at 6%