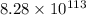Answer :
(a) The value of Gibbs free energy for the reaction is
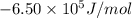
(b) The value of
 at 298 is,
at 298 is,
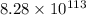
Explanation :
The given cell reaction is:
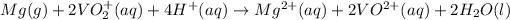
The half reaction will be:
Reaction at anode (oxidation) :

Reaction at cathode (reduction) :
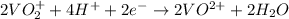
First we have to calculate the Gibbs free energy.
Formula used :
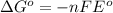
where,
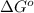 = Gibbs free energy = ?
= Gibbs free energy = ?
n = number of electrons = 2 (from the reaction)
F = Faraday constant = 96500 C/mole
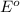 = standard e.m.f of cell = 3.37 V
= standard e.m.f of cell = 3.37 V
Now put all the given values in this formula, we get the Gibbs free energy.
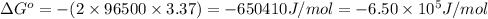
Thus, the value of Gibbs free energy for the reaction is
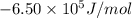
Now we have to calculate the value of equilibrium constant.
Formula used :
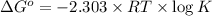
where,
R = universal gas constant = 8.314 J/K/mole
T = temperature =
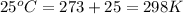
K = equilibrium constant = ?
Now put all the given values in this formula, we get the value of
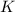
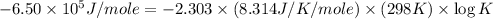
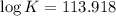
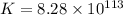
Therefore, the value of
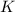 at 298 is,
at 298 is,