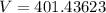Question

Consider the following.y = 5xe?x, y = 0, x = 2; about the y-axis(a) Set up an integral for the volume V of the solid obtained by rotating the region bounded by the given curve about the specified axis.(b) Use your calculator to evaluate the integral correct to five decimal places

Answer 1

The volume for the solid of revolution is
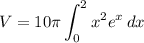`V=\displaystyle 10\pi\int_0^2 x^2e^x\, dx` and its value is 401.43623.

Explanation:

Since the function is rotating over the y-axis and it is a function in terms of x we can use Shell integration which general formula is given by

`V=2\pi \int\limits^a_b {x f(x)} \, dx`

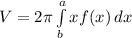
a) Setting up the integral.

We are given one end point for x which is x = 2, but we are not given the other, so we can set y = 0 on the given equation to get:

`0  = 5xe^x`

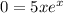
Notice that the exponential function is not going to be equal to 0, so we get the other endpoint for the interval as

`0 = 5x`

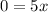
which give us

`x=0`

Thus we integate from x = 0 to 2, so we will get:

`V=\displaystyle 2\pi\int_0^2 x (5x)e^x\, dx`

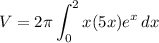
And we can simplify that to

`V=\displaystyle 10\pi\int_0^2 x^2e^x\, dx`

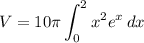
b) Using a calculator to evaluate the integral.

We can use a calculator to write the integral including the interval to get:

`V = 20 \left(e^2-1\right) \pi`

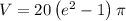
And its value rounded to 5 decimal places is

`V=401.43623`