Question

Small rockets are used to make tiny adjustments in the speeds of satellites. One such rocket has a thrust of 35 N. If it is fired to change the velocity of a 72300 kg spacecraft by 60 cm/s, how long should it be fired?

Answer 1

To solve this problem it is necessary to apply the concepts related to the Moment. The momentum represents the product of the mass and velocity of an object, that is

`p = mv`

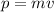
where

m = mass

v = velocity

At the same time using Newtonian relations, we can consider the Moment's equivalence as a function of Force and time as

p = Ft

Where

F = Force

t = time

Matching the two expressions we get that

`mv = Ft`

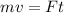
Re-arrange to find t,

`t = (mv)/(F)`

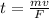
Our values are given as

`m = 72300kg`

`F = 35N`

`v = 60cm/s((1m)/(100cm))\rightarrow v = 0.6m/s`

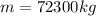
Replacing we have that the time is

`t = (mv)/(F)`

`t = ((72300)(0.6))/(35)`

`t = 1239.4s`

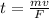
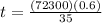
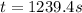
Therefore would be take 1239.4s