Answer: They could not have managed to stay afloat on the raft together
Step-by-step explanation:
A body is able to float in a liquid if its weight is less than the maximum buoyant force
 , when this condition is not fulfilled the body is submerged.
, when this condition is not fulfilled the body is submerged.
So, the buoyant force for the piece of furniture in seawater is given by:
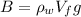 (1)
(1)
Where:
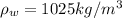 is the density of seawater
is the density of seawater
 is the displaced volume of the furniture in seawater, which can be found knowing the dimensions of the piece: Area:
is the displaced volume of the furniture in seawater, which can be found knowing the dimensions of the piece: Area:
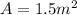 , depth:
, depth:
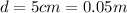 . Then
. Then
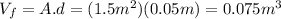
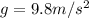 is the acceleration due gravity
is the acceleration due gravity
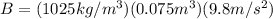 (2)
(2)
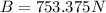 (3) This is the buoyant force with the table alone, now let's calculate the weight of Jack and Rose and evaluate if their weights added to te piece of furniture fulfill the condition given above
(3) This is the buoyant force with the table alone, now let's calculate the weight of Jack and Rose and evaluate if their weights added to te piece of furniture fulfill the condition given above
Furniture's weight:
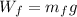 (4)
(4)
Where
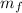 is the mass of the piece of furniture, which can be calculated knowing its density
is the mass of the piece of furniture, which can be calculated knowing its density
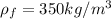 and volume
and volume
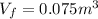
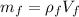 (5)
(5)
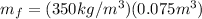 (6)
(6)
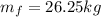 (7)
(7)
Hence
 (8) As we can see
(8) As we can see
 which means the weight of the furniture is less than the buoancy force and is able to float
which means the weight of the furniture is less than the buoancy force and is able to float
Rose's weight:
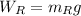 (9)
(9)
Where
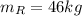 is Rose's mass
is Rose's mass
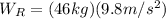 (10)
(10)
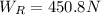 (11)
(11)
Jack's weight:
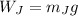 (12)
(12)
Where
 is Jack's mass
is Jack's mass
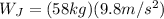 (13)
(13)
 (14)
(14)
Rose + Furniture weight:
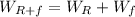 (15)
(15)
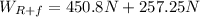 (16)
(16)
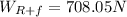 (17) As we can see
(17) As we can see
 which means the weight of both Rose and the furniture is less than the buoancy force, so Rose would not drown
which means the weight of both Rose and the furniture is less than the buoancy force, so Rose would not drown
Jack + Furniture weight:
 (18)
(18)
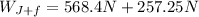 (19)
(19)
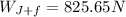 (20) As we can see
(20) As we can see
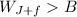 which means the weight of both Jack and the furniture is greater than the buoancy force and do not fulfill the condition.
which means the weight of both Jack and the furniture is greater than the buoancy force and do not fulfill the condition.
Hence Jack would drown
Jack + Rose + Furniture weight:
 (21)
(21)
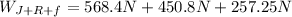 (22)
(22)
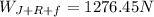 (23) As we can see
(23) As we can see
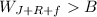 which means the combined weight of Jack, Rose and the furniture is greater than the buoancy force and do not fulfill the condition.
which means the combined weight of Jack, Rose and the furniture is greater than the buoancy force and do not fulfill the condition.
Hence, Jack and Rose could not have managed to stay afloat on the raft together.
In fact, according to the calculations Jack did not have options to survive anyway :(