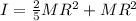Answer:

Step-by-step explanation:
For answer this we will use the paralell axis theorem:
I=
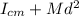
Where
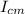 is the moment of inertia of the center of mass, M is the mass of the sphere and d is the distance between the center of mass and the axis for rotate, then:
is the moment of inertia of the center of mass, M is the mass of the sphere and d is the distance between the center of mass and the axis for rotate, then: