Question

Are the functions of g(x)=(x-4)^2 and h(x)=x^2-4 equivalent? Explain your reasoning.

Answer 1

`g(x) = (x-4)^2\; and \;h(x)= x^2-4 \;are\;\bold{not}\;equivalent`

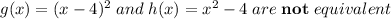
Explanation:

For two functions g(x) and h(x) to be equivalent, they must have the same domain and range.

Domain is the set of all values of x(inputs) that result in a real and defined value for the function

Range is the set of all values of the function that it can take given the values of x in the domain

`g(x)=(x-4)^2=16-8x+x^2\\`

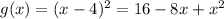
Can be rewritten as

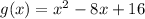`g(x) = x^2 -8x + 16` The domain of g is unrestricted, g can be any value so the

Domain of g:
`-\infty < x < \infty`
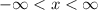
Range of g: Since
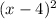`(x-4)^2` is always positive including 0, the range of g(x) is g(x) ≥ 0

`h(x) = x^2 - 4`

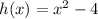
Domain of h :
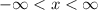`-\infty < x < \infty` since x can be any value and we will still get a real number as function output

However x² is always zero or a positive number so we have the restriction
x² ≥ 0

Subtract 4 on both sides

x²-4 >= -4

But the above is nothing but the outputs of h(x)

So h(x) >= -4 and can be written as -4 ≤ x ≤ ∞

So we can see that, while the domains of the two functions are the same, their ranges are different

Hence the two functions g(x) and h(x) are not equivalent

Tip
If you have difficulty determining domain and range, take a specific value of x for both functions and check if the function output values are the same. It may not always be easy choosing an appropriate x value depending on the function

For x = 0

g(0) = (0-4)² = (-4)² = 16

h(0) = 0^2 -4 = 0-4 = -4

So we get different output values for the same input value for both functions and therefore they are not equivalent

You can this latter explanation to the above explanation

Hope that helps and is understandable :)