Question

A grating with 410 grooves/mm is used with an incandescent light source. Assume the visible spectrum to range in wavelength from 400 nm to 700 nm. How many orders can one see the entire visible spectrum

Answer 1

To solve this problem it is necessary to apply the Bragg's law which allows to study the directions in which the diffraction of X-rays on the surface of a crystal produces constructive interference.

Extrapolating the equation and obtaining its mathematical meaning we have to

`dsin\theta = n\lambda`

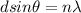
Where

d = Separation between slits

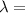`\lambda =` wavelength

n = Order number representing the number of repetition of the spectrum

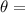`\theta =` Angle between the source and the screen at this case are perpendicular

At the same time we have that the grating for this case is given as

`d = (1)/(N) = (1)/(410*10^(-3))m = 2.439*10^(-6)m`

Using the previous equation to find the order number we have that

`dsin\theta = n\lambda`

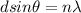
For the first wavelength

`n_(red) = (dsin\theta)/(\lambda_1)`

`n_(red) = ((2.439*10^(-6))(sin90))/(700*10^(-9))`

`n_(red) = 3.4842`

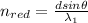
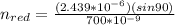
For the second wavelength

`n_(violet) = (dsin\theta)/(\lambda_2)`

`n_(violet) = ((2.439*10^(-6))(sin90))/(400*10^(-9))`

`n_(violet) = 6.0975`

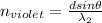
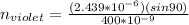
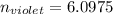
Therefore the number of orders in which the visible spectrum exists is

`\Delta n = n_(violet)-n_(red)`

`\Delta n = 6.0975-3.4842`

`\Delta n = 2.6133 \approx 3`

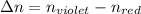
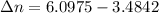
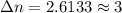
Therefore the number of order can one see the entire visible spectrum 3.