Question

How long will it take a sample of radioactive substance to decay to half of its original amount, if it decays according to the function A(t) = 350e-0.169t, where t is the time in years? Round your answer to the nearest hundredth year.

Answer 1

4.101 yrs

Explanation:

Given that a sample of radioactive substance to decay has the following exponential function.

`A(t)=350e^(-0.169t)`

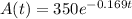
where t= no of years lapsed

When t=0 i.e. initially we have population as

`A(0) = 350`

When it becomes half we have

=
`A(t) = 175 =  350e^(-0.169t)\\0.5= e^(-0.169t)\\`

Taking log to base e we have

`-0.169t = ln (0.5) \\t=4.101`

In approximately 4.101 years the population decays to half