Question

(1) A manufacturer of tires believes that their mean time to failure (MTTF) is 20 613 km. They also believe that time to failure (TTF) is normally distributed with a standard deviation of 512 km (a) If the manufacturer wants to honor a 20 000 km warranty, what is the probability that any tire will fail within the warranty period? (b) What does the warranty period need to be to ensure that no more than 5 per cent of tires fail in the warranty period

Answer 1

a) The probability of falling in the warranty period is 11.6%.

b) The warranty period need to be 19771 km to ensure that no more than 5 per cent of tires fail in the warranty period.

Explanation:

a) To fall within the warranty period, the tire has to fail before the 20,000 km.

To calculate the probability, we first calculate the z-value:

`z=(X-\mu)/(\sigma)=(20000-20613)/(512)=  (-613)/(512)= -1.197`

Then, the probability of falling in the warranty period is:

`P(X<20,000)=P(z<-1.197)=0.116`

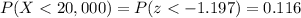
b) To calculate this we have to go on from a P(z<z₁)=0.05. This happens for z=-1.645.

This corresponds to a value X of:

`X=\mu+z*\sigma=20613+(-1.645)*512=20613-842=19771`

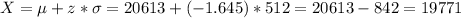
The warranty period need to be 19771 km to ensure that no more than 5 per cent of tires fail in the warranty period.