m₁ is 4.37 kg and m₂ is 1.03 kg
Step-by-step explanation:
Sum of masses = m₁ + m₂ = 5.40 kg
m₂ = 5.4 - m₁
We have gravitational force
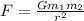
G = 6.674 x 10⁻¹¹ Nm²/kg²
r = 18.5 cm = 0.185 m
F = 8.80 x 10⁻⁹ N
Substituting,

m₁ x (5.4-m₁) = 4.513
5.4m₁ - m₁² = 4.513
m₁² - 5.4m₁ + 4.513 = 0
m₁ = 4.37kg or m₁ = 1.03 kg
If m₁ = 4.37 kg we have
m₂ = 1.03 kg
If m₁ = 1.03 kg we have
m₂ = 4.37 kg
So Let us consider
m₁ = 4.37 kg and m₂ = 1.03 kg