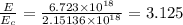Answer:
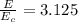
Step-by-step explanation:
The kinetic energy of a rigid body that travels at a speed v is given by the expression:
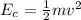
The equivalence between mass and energy established by the theory of relativity is given by:
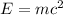
This formula states that the equivalent energy
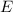 can be calculated as the mass
can be calculated as the mass
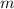 multiplied by the speed of light
multiplied by the speed of light
 squared.
squared.
Where
 is approximately
is approximately
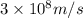
Hence:
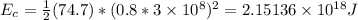
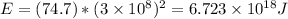
Therefore, the ratio of the person's relativistic kinetic energy to the person's classical kinetic energy is: