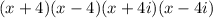Answer:
(x+4)(x-4)(x+4i)(x-4i) (answer D)
Explanation:
We can re-write the original binomial as a difference of squares noticing that
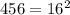 and that
and that
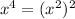
Then we have:
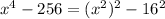
Then we can factor this out using the difference of squares factor form:
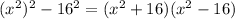
Now,
 , is itself a difference of squares which we can factor out further:
, is itself a difference of squares which we can factor out further:
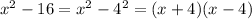
And we can also solve for the binomial:
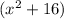 :
:
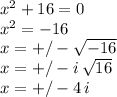
then we can write
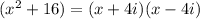
Therefore, the final factor form of the original binomial is the product of all factors we found: