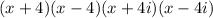Question

Which of these represents the factorization of x4−256 ?

A
(x−4)2(x+4)2

B
(x−4i)2(x+4i)2

C
(x−4)2(x+4i)2

D
(x−4)(x+4)(x−4i)(x+4i)

Answer 1

(x+4)(x-4)(x+4i)(x-4i) (answer D)

Explanation:

We can re-write the original binomial as a difference of squares noticing that
`456=16^2` and that
`x^4=(x^2)^2`

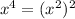
Then we have:

`x^4-256=(x^2)^2-16^2`

Then we can factor this out using the difference of squares factor form:

`(x^2)^2-16^2=(x^2+16)(x^2-16)`

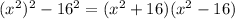
Now,
`(x^2-16)`, is itself a difference of squares which we can factor out further:
`x^2-16=x^2-4^2=(x+4)(x-4)`

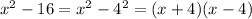
And we can also solve for the binomial:
`(x^2+16)`:

`x^2+16=0\\x^2=-16\\x=+/-√(-16) \\x=+/-i\,√(16) \\x=+/-4\,i`

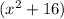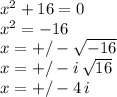
then we can write
`(x^2+16)=(x+4i)(x-4i)`

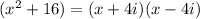
Therefore, the final factor form of the original binomial is the product of all factors we found:
`(x+4)(x-4)(x+4i)(x-4i)`