Question

A sample contains 100 g of a radioactive isotope. How much radioactive

isotope will remain in the sample after 2 half-lives? OA. 50 g
OB. 25 g
OC. 75 g
OD. 100 g

Answer 1

its 12.5 g for anyone else who had different options

Step-by-step explanation:

Answer 2

B. 25 g

Step-by-step explanation:

Given:

The initial mass of radioactive isotope is,
`m_0=100\ g`

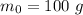
There is exponential decay of the isotope with time.

Half life means the time in which the given mass reduces by half. For every half life, the mass reduces by half of the previous mass.

So, for the first half life, the mass that remains is given as:

`m_1=(m_0)/(2)=(100)/(2)=50\ g`

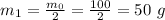
Now, for the second half life, the mass 50 g is again reduced to half.

So, the mass that remains after 2 half-lives is given as:

`m_2=(m_1)/(2)=(50)/(2)=25\ g`

Therefore, the radioactive isotope that will remain in the sample after 2 half-lives is 25 g.