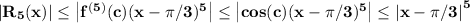Answer:
See below
Explanation:
Remark:
This is the complete question
Given f(x) = sin x , a =π/6, n=4, 0<x< π/3
a. approximate f by a Taylor polynomial with degree n at the number a
b. use Taylor's inequality to estimate the accuracy of the approximation f(x) ~ Tn(x) when x lies in the given interval .
_________________________________
Answer:
Recall Taylor's approximation with a polynomial for a function f if we know the value of f at a point a and there exists the derivatives involved:
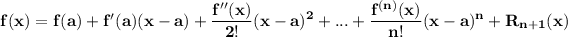
where
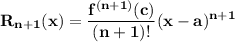
for some c such that c < | a-x |
Now, if f(x) = sin(x) and a =π/6 we have
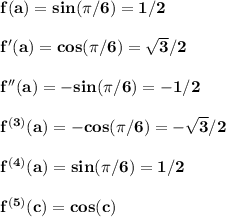
and we can approximate sin(x) with the polynomial
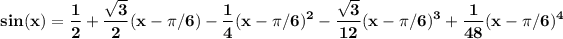
The error of the approximation when x lies in the interval 0<x< π/3 can be bounded by