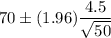Question

Management of a particular golf course wants to know what the average score is for their course. It is known that from previous games that the standard deviation of the golf scores is 4.5. To estimate the average score, the managers took a random sample of 50 golfers and found that it has a mean of 70, Use a 95% confidence interval (CI) to estimate the true average score of golfers on this particular course. a.70 (1.645)4.5/S0) O b. 701 ( 1 .96)(4.5) ? ?. 70 (1.96)(4.5 /V50) od. cannot compute

Answer 1

Answer: c.
`70\pm (1.96)(4.5)/(√(50))`

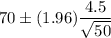
Explanation:

The confidence interval for population mean is given by :-

`\overline{x}\pm z^*(\sigma)/(√(n))`

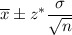
, where n= sample size

`\overline{x}` = sample mean.

z*= Critical value.

`\sigma`= population standard deviation.

As per given , we have

n= 50

`\sigma=4.5`

`\overline{x}=70`

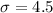
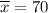
Also, we know that the critical value for 95% confidence interval : z*= 1.96

Then, the 95% confidence interval (CI) to estimate the true average score of golfers on this particular course will be :

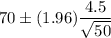`70\pm (1.96)(4.5)/(√(50))` (substitute all the value in the above formula.)

Hence, the correct option is c.
`70\pm (1.96)(4.5)/(√(50))`