Answer:
The probability that the regulations will NOT be met is (c)- 8%
Explanation:
The standard deviation information in the question is wrong. It is not 7, It should be 0.7
the probability that the regulations will NOT be met for the plane loaded with 100 boxes of goods is
=P(X>3.3 kg) where 3.3 is the mean weight of the 100 boxes in the plane.
=P(z>z*) where z* is the statistic of 3.30 kg in the weight distribution.
z* can be calculated as
z*=
 where
where
- X is the cutoff mean weight of the boxes the airplane cannot exceed (3.3 kg)
- M is the mean weight of the boxes (3.2)
- s is the standard deviation (0.7 kg)
- N is the sample size (100)
then z*=
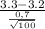 ≈ 1.43
≈ 1.43
then P(z>z*)≈0.08 or 8%