Question

If you have 0.391 m 3 of water at 25.0 ∘ C and add 0.117 m 3 of water at 95.0 ∘ C , what is the final temperature of the mixture? Use 1000 kg/m 3 as the density of water at any temperature.

Answer 1

In order to solve this problem, it is necessary to apply the concepts related to density, as a function of volume and mass, as well as the principle of calorimetry.

By definition we know that Density is given as a function of mass in a given volume, mathematically it can be expressed as

`\rho = (m)/(V)`

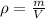
Where,

m = mass

V = Volume

Re-arrange to find the respective mass at each state we have

`m = \rho V`

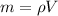
For state 1 we have that the mass is

`m_1 = (1000kg/m^3)(0.391m^3) = 391kg`

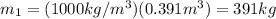
For state 2

`m_2 = (1000kg/m^3)(0.117m^3) = 117kg`

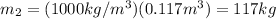
Now from calorimetry we know that heat change is given under

`Q = mc_p\Delta T`

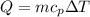
For energy conservation then,

`m_1c_p\Delta T = m_2c_p\Delta T`

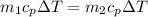
Since the specific heat is the same for the fluid then,

`m_1\Delta T = m_2\Delta T`

`(391) (T-25\°C) = (117) (95\°C-T)`

`T = 41.12\°C`

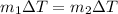
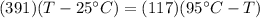
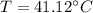
Therefore the final temperature of the mixture will be 41.12°C