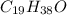Answer : The molecular formula of a compound is,
Solution :
If percentage are given then we are taking total mass is 100 grams.
So, the mass of each element is equal to the percentage given.
Mass of C = 80.78 g
Mass of H = 13.56 g
Mass of O = 5.66 g
Molar mass of C = 12 g/mole
Molar mass of H = 1 g/mole
Molar mass of O = 16 g/mole
Step 1 : convert given masses into moles.
Moles of C =
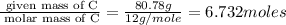
Moles of H =
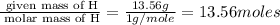
Moles of O =
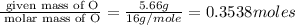
Step 2 : For the mole ratio, divide each value of moles by the smallest number of moles calculated.
For C =
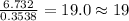
For H =
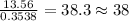
For O =
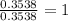
The ratio of C : H : O = 19 : 38 : 1
The mole ratio of the element is represented by subscripts in empirical formula.
The Empirical formula =
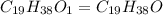
The empirical formula weight = 19(12) + 38(1) + 1(16) = 282 gram/eq
Now we have to calculate the molar mass of pheromone.
Formula used :

where,
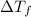 = change in freezing point
= change in freezing point
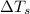 = freezing point of solution =
= freezing point of solution =
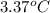
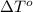 = freezing point of benzene =
= freezing point of benzene =
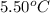
i = Van't Hoff factor = 1 (for non-electrolyte)
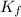 = freezing point constant for benzene =
= freezing point constant for benzene =
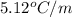
m = molality
Now put all the given values in this formula, we get
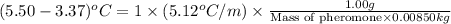
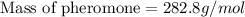
Now we have to calculate the molecular formula of the compound.
Formula used :
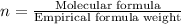
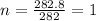
Molecular formula =
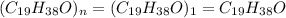
Therefore, the molecular of the compound is,