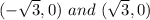Question

X-intercept and y-intercepts og y=x^2-3

Answer 1

Part 1) The y-intercept is the point
`(0,-3)`

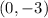
Part 2) The x-intercepts are the points
`(-√(3),0)\ and\ (√(3),0)`

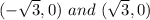
Explanation:

we have

`y=x^(2)-3`

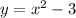
This is a vertical parabola open upward

step 1

Find the y-intercept

we know that

The y-intercept is the value of y when the value of x is equal to zero

so

For x=0

`y=(0)^(2)-3`

`y=-3`

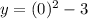
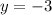
The y-intercept is the point (0,-3)

step 2

Find the x-intercepts

we know that

The x-intercept is the value of x when the value of y is equal to zero

so

For y=0

`x^(2)-3=0`

solve for x

Adds 3 both sides

`x^(2)-3+3=0+3`

`x^(2)=3`

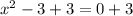
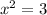
take square root both sides

`x=(+/-)√(3)`

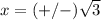
so

The x-intercepts are the points
`(-√(3),0)\ and\ (√(3),0)`